Elastis atau elastisitas adalah kemampuan sebuah benda untuk kembali ke bentuk awalnya ketika gaya luar yang diberikan pada benda tersebut dihilangkan. Jika sebuah gaya diberikan pada sebuah benda yang elastis, maka bentuk benda tersebut berubah. Untuk pegas dan karet, yang dimaksudkan dengan perubahan bentuk adalah pertambahan panjang. Benda-benda elastis juga memiliki batas elastisitas. Ada 2 macam benda yaitu: benda elastis dan benda plastis (tak elastis).

1. HUKUM HOOKE
Pertambahan panjang yang timbul berbanding lurus dengan gaya tarik yang diberikan. Hal ini pertama kali diselidiki pada abad 17 oleh seorang arsitek berkebangsaan Inggris yang bernama Robert Hooke. Hooke menyelidiki hubungan antara gaya tarik yang diberikan pada sebuah pegas dengan pertambahan panjang pegas tersebut.
Hooke menemukan bahwa pertambahan panjang pegas yang timbul berbanding lurus dengan gaya yang diberikan.
F x
Lebih jauh lagi, Hooke juga menemukan bahwa pertambahan panjang pegas sangat bergantung pada karakteristik dari pegas tersebut. Pegas yang mudah teregang seperti karet gelang akan mengalami pertambahan panjang yang besar meskipun gaya yang diberikan kecil. Sebaliknya pegas yang sangat sulit teregang seperti pegas baja akan mengalami pertambahan panjang yang sedikit saja meskipun diberi gaya yang besar. Karakteristik yang dimiliki masing-masing pegas ini dinyatakan sebagai tetapan gaya dari pegas tersebut. Pegas yang mudah teregang seperti karet gelang memiliki tetapan gaya yang kecil. Sebaliknya pegas yang sulit teregang seperti pegas baja memiliki tetapan gaya yang besar. Secara umum apa yang ditemukan Hooke bisa dinyatakan sebagai berikut:
F = k. x
Keterangan:
F = gaya yang diberikan pada pegas (N)
k = tetapan gaya pegas (N/m)
x = pertambahan panjang pegas (m)

2. ENERGI POTENSIAL PEGAS
Besar energi potensial sebuah pegas dapat dihitung dari grafik hubungan gaya yang bekerja pada pegas dengan pertambahan panjang pegas tersebut.
Ep = ½ F . x
= ½ (k . x) . x

Keterangan:
Ep = energi potensial pegas (joule)
k = tetapan gaya pegas (N/m)
x = pertambahan panjang pegas (m)

3. Modulus Elastisitas
Yang dimaksud dengan Mosdulus Elastisitas adalah perbandingan antara tegangan dan regangan. Modulus ini dapat disebut dengan sebutan Modulus Young.

Tegangan (Stress)
Tegangan adalah gaya per satuan luas penampang. Satuan tegangan adalah N/m²
Regangan (Strain)
Regangan adalah perbandingan antara pertambahan panjang suatu batang terhadap panjang awal mulanya bila batang itu diberi gaya.

4. Rangkaian Pegas
Suatu rangakaian pegas pada dasarnya tersusun dari susunan seri dan / atau susunan paralel.
1) Susunan Seri
Saat pegas dirangkai seri, gaya tarik yang dialami tiap pegas sama besarnya dan gaya tarik ini = gaya tarik yang dialami pegas pengganti ( F1 = F2 = ....Fn). Pertambahan panjang pegas pengganti seri = total pertambahan panjang tiap – tiap pegas ( = x1 + x2 + ..... xn) maka nilai konstanta pengganti = total dari kebalikan tiap – tiap tetapan pegas ( 1/ks = 1/k1 + 1/k2 + ....1/kn ).
2) Susunan Paralel
Saat pegas dirangkai paralel, gaya tarik pada pegas pengganti F = total gaya tarik pada tiap pegas ( F = F1 + F2 + ....F ). Pertambahan panjang tiap pegas sama besarnya ( xtotal = x1 + x2 + ..... xn ) maka nilai konstanta pengganti = total dari tetapan tiap – tiap pegas (kp = k1 + k2 + .... kn).

5. Gerak Benda di Bawah Pengaruh Gaya Pegas
Bila suatu benda yang digantungkan pada pegas ditarik sejauh x meter dan kemudian dilepas, maka benda akan bergetar.

Hukum Hooke dan Elastisitas

Pengantar

Pernakah dirimu melihat alat yang tampak pada gambar ini ? wah, hari gini belum itu adalah gambar pegas. Nyamannya kehidupan kita tidak terlepas dari bantuan pegas, walaupun kadang tidak kita sadari. Ketika dirimu mengendarai sepeda motor atau berada dalam sebuah mobil yang sedang bergerak di jalan yang permukaannya tidak rata alias jalan berlubang, pegas membantu meredam kejutan sehingga dirimu merasa sangat nyaman berada dalam mobil atau ketika berada di atas sepeda motor. Apabila setiap kendaraan yang anda tumpangi tidak memiliki pegas, yakinlah perjalanan anda akan sangat melelahkan, apalagi ketika menempuh perjalanan yang jauh. Ketika turun dari mobil langsung meringis kesakitan karena terserang encok dan pegal linu

pegas tidak hanya dimanfaatkan di mobil atau sepeda motor, tetapi pada semua kendaraan yang selalu kita gunakan. Selengkapnya akan kita kupas tuntas pada akhir tulisan ini. Pegas merupakan salah satu contoh benda elastis. Contoh benda elastis lainnya adalah karet mainan

(kalo karet pasti tahu

). Btw, elastis itu apa ya ? terus apa hubungan antara elastis dan hukum Hooke ? Nah, sekarang bersiap-siaplah untuk melakukan pertempuran dengan ilmu fisika. Siapkanlah amunisi sebanyak-banyaknya; sapu tangan atau tisu untuk ngelap keringat, obak sakit kepala dkk… Selamat belajar ya, semoga dirimu memenangi pertempuran ini

ELASTISITAS

Ketika dirimu menarik karet mainan sampai batas tertentu, karet tersebut bertambah panjang. silahkan dicoba kalau tidak percaya. Jika tarikanmu dilepaskan, maka karet akan kembali ke panjang semula. Demikian juga ketika dirimu merentangkan pegas, pegas tersebut akan bertambah panjang. tetapi ketika dilepaskan, panjang pegas akan kembali seperti semula. Apabila di laboratorium sekolah anda terdapat pegas, silahkan melakukan pembuktian ini. Regangkan pegas tersebut dan ketika dilepaskan maka panjang pegas akan kembali seperti semula. Mengapa demikian ? hal itu disebabkan karena benda-benda tersebut memiliki sifat elastis. Elastis atau elastsisitas adalah kemampuan sebuah benda untuk kembali ke bentuk awalnya ketika gaya luar yang diberikan pada benda tersebut dihilangkan. Jika sebuah gaya diberikan pada sebuah benda yang elastis, maka bentuk benda tersebut berubah. Untuk pegas dan karet, yang dimaksudkan dengan perubahan bentuk adalah pertambahan panjang.

Perlu anda ketahui bahwa gaya yang diberikan juga memiliki batas-batas tertentu. Sebuah karet bisa putus jika gaya tarik yang diberikan sangat besar, melawati batas elastisitasnya. Demikian juga sebuah pegas tidak akan kembali ke bentuk semula jika diregangkan dengan gaya yang sangat besar. Jadi benda-benda elastis tersebut memiliki batas elastisitas. Batas elastis itu apa ? lalu bagaimana kita bisa mengetahui hubungan antara besarnya gaya yang diberikan dan perubahan panjang minimum sebuah benda elastis agar benda tersebut bisa kembali ke bentuk semula ? untuk menjawab pertanyaan ini, mari kita berkenalan dengan paman Hooke.

HUKUM HOOKE

Hukum Hooke pada Pegas

Misalnya kita tinjau pegas yang dipasang horisontal, di mana pada ujung pegas tersebut dikaitkan sebuah benda bermassa m. Massa benda kita abaikan, demikian juga dengan gaya gesekan, sehingga benda meluncur pada permukaan horisontal tanpa hambatan. Terlebih dahulu kita tetapkan arah positif ke kanan dan arah negatif ke kiri. Setiap pegas memiliki panjang alami, jika pada pegas tersebut tidak diberikan gaya. Pada kedaan ini, benda yang dikaitkan pada ujung pegas berada dalam posisi setimbang (lihat gambar a). Untuk semakin memudahkan pemahaman dirimu,sebaiknya dilakukan juga percobaan.

Apabila benda ditarik ke kanan sejauh +x (pegas diregangkan), pegas akan memberikan gaya pemulih pada benda tersebut yang arahnya ke kiri sehingga benda kembali ke posisi setimbangnya (gambar b).

Sebaliknya, jika benda ditarik ke kiri sejauh -x, pegas juga memberikan gaya pemulih untuk mengembalikan benda tersebut ke kanan sehingga benda kembali ke posisi setimbang (gambar c).

Besar gaya pemulih F ternyata berbanding lurus dengan simpangan x dari pegas yang direntangkan atau ditekan dari posisi setimbang (posisi setimbang ketika x = 0). Secara matematis ditulis :

Persamaan ini sering dikenal sebagai persamaan pegas dan merupakan hukum hooke. Hukum ini dicetuskan oleh paman Robert Hooke (1635-1703). k adalah konstanta dan x adalah simpangan. Tanda negatif menunjukkan bahwa gaya pemulih alias F mempunyai arah berlawanan dengan simpangan x. Ketika kita menarik pegas ke kanan maka x bernilai positif, tetapi arah F ke kiri (berlawanan arah dengan simpangan x). Sebaliknya jika pegas ditekan, x berarah ke kiri (negatif), sedangkan gaya F bekerja ke kanan. Jadi gaya F selalu bekeja berlawanan arah dengan arah simpangan x. k adalah konstanta pegas. Konstanta pegas berkaitan dengan elastisitas sebuah pegas. Semakin besar konstanta pegas (semakin kaku sebuah pegas), semakin besar gaya yang diperlukan untuk menekan atau meregangkan pegas. Sebaliknya semakin elastis sebuah pegas (semakin kecil konstanta pegas), semakin kecil gaya yang diperlukan untuk meregangkan pegas. Untuk meregangkan pegas sejauh x, kita akan memberikan gaya luar pada pegas, yang besarnya sama dengan F = +kx. Hasil eksperimen menunjukkan bahwa x sebanding dengan gaya yang diberikan pada benda.

Hukum Hooke untuk benda non Pegas

Hukum hooke ternyata berlaku juga untuk semua benda padat, dari besi sampai tulang tetapi hanya sampai pada batas-batas tertentu. Mari kita tinjau sebuah batang logam yang digantung vertikal, seperti yang tampak pada gambar di bawah.

Pada benda bekerja gaya berat (berat = gaya gravitasi yang bekerja pada benda), yang besarnya = mg dan arahnya menuju ke bawah (tegak lurus permukaan bumi). Akibat adanya gaya berat, batang logam tersebut bertambah panjang sejauh (delta L)

Jika besar pertambahan panjang (delta L) lebih kecil dibandingkan dengan panjang batang logam, hasil eksperimen membuktikan bahwa pertambahan panjang (delta L) sebanding dengan gaya berat yang bekerja pada benda. Perbandingan ini dinyatakan dengan persamaan :

Persamaan ini kadang disebut sebagai hukum Hooke. Kita juga bisa menggantikan gaya berat dengan gaya tarik, seandainya pada ujung batang logam tersebut tidak digantungkan beban.

Besarnya gaya yang diberikan pada benda memiliki batas-batas tertentu. Jika gaya sangat besar maka regangan benda sangat besar sehingga akhirnya benda patah. Hubungan antara gaya dan pertambahan panjang (atau simpangan pada pegas) dinyatakan melalui grafik di bawah ini.

Jika sebuah benda diberikan gaya maka hukum Hooke hanya berlaku sepanjang daerah elastis sampai pada titik yang menunjukkan batas hukum hooke. Jika benda diberikan gaya hingga melewati batas hukum hooke dan mencapai batas elastisitas, maka panjang benda akan kembali seperti semula jika gaya yang diberikan tidak melewati batas elastisitas. tapi hukum Hooke tidak berlaku pada daerah antara batas hukum hooke dan batas elastisitas. Jika benda diberikan gaya yang sangat besar hingga melewati batas elastisitas, maka benda tersebut akan memasuki daerah plastis dan ketika gaya dihilangkan, panjang benda tidak akan kembali seperti semula; benda tersebut akan berubah bentuk secara tetap. Jika pertambahan panjang benda mencapai titik patah, maka benda tersebut akan patah.

Berdasarkan persamaan hukum Hooke di atas, pertambahan panjang (delta L) suatu benda bergantung pada besarnya gaya yang diberikan (F) dan materi penyusun dan dimensi benda (dinyatakan dalam konstanta k). Benda yang dibentuk oleh materi yang berbeda akan memiliki pertambahan panjang yang berbeda walaupun diberikan gaya yang sama, misalnya tulang dan besi. Demikian juga, walaupun sebuah benda terbuat dari materi yang sama (besi, misalnya), tetapi memiliki panjang dan luas penampang yang berbeda maka benda tersebut akan mengalami pertambahan panjang yang berbeda sekalipun diberikan gaya yang sama. Jika kita membandingkan batang yang terbuat dari materi yang sama tetapi memiliki panjang dan luas penampang yang berbeda, ketika diberikan gaya yang sama, besar pertambahan panjang sebanding dengan panjang benda mula-mula dan berbanding terbalik dengan luas penampang. Makin panjang suatu benda, makin besar besar pertambahan panjangnya, sebaliknya semakin tebal benda, semakin kecil pertambahan panjangnya. Jika hubungan ini kita rumuskan secara matematis, maka akan diperoleh persamaan sebagai berikut :

Persamaan ini menyatakan hubungan antara pertambahan panjang (delta L) dengan gaya (F) dan konstanta (k). Materi penyusun dan dimensi benda dinyatakan dalam konstanta k. Untuk materi penyusun yang sama, besar pertambahan panjang (delta L) sebanding dengan panjang benda mula-mula (L_o) dan berbanding terbalik dengan luas penampang (A). Kalau dirimu bingung dengan panjang mula-mula atau luas penampang, coba amati gambar di bawah ini terlebih dahulu.

Dah paham panjang mula-mula (L_o) dan luas penampang (A) ?... Lanjut ya …

Besar E bergantung pada benda (E merupakan sifat benda). Secara matematis akan kita turunkan nanti… tuh di bawah

Pada persamaan ini tampak bahwa pertambahan panjang (delta L) sebanding dengan hasil kali panjang benda mula-mula (Lo) dan Gaya per satuan Luas (F/A).

Tegangan

Gaya per satuan Luas disebut juga sebagai tegangan. Secara matematis ditulis :

Satuan tegangan adalah N/m² (Newton per meter kuadrat)

Regangan

Regangan merupakan perbandingan antara perubahan panjang dengan panjang awal. Secara matematis ditulis :

Karena L sama-sama merupakan dimensi panjang, maka regangan tidak mempunyai satuan (regangan tidak mempunyai dimensi).

Regangan merupakan ukuran perubahan bentuk benda dan merupakan tanggapan yang diberikan oleh benda terhadap tegangan yang diberikan. Jika hubungan antara tegangan dan regangan dirumuskan secara matematis, maka akan diperoleh persamaan berikut :

Ini adalah persamaan matematis dari Modulus Elastis (E) alias modulus Young (Y). Jadi modulus elastis sebanding dengan Tegangan dan berbanding terbalik Regangan.

Di bawah ini adalah daftar modulus elastis dari berbagai jenis benda padat

Referensi :
Giancoli, Douglas C. 2001. Fisika Jilid I (Terjemahan). Jakarta : Penerbit Erlangga.
Halliday dan Resnick. 1991. Fisika Jilid I (Terjemahan). Jakarta : Penerbit Erlangga.
Tipler, P.A. 1998. Fisika untuk Sains dan Teknik-Jilid I (Terjemahan). Jakarta : Penebit Erlangga.
Young, Hugh D. & Freedman, Roger A. 2002. Fisika Universitas (Terjemahan). Jakarta : Penerbit Erlangga.
Sumber: http://www.gurumuda.com/hukum-hooke-elastisitas

Hukum Hooke adalah hukum atau ketentuan mengenai gaya dalam bidang ilmu fisika yang terjadi karena sifat elastisitas dari sebuah pir atau pegas. Besarnya gaya Hooke ini secara proporsional akan berbanding lurus dengan jarak pergerakan pegas dari posisi normalnya, atau lewat rumus matematis dapat digambarkan sebagai berikut:

$\mathbf{F}=-k\mathbf{x}$

di mana

F adalah gaya (dalam unit newton); k adalah konstante pegas (dalam newton per meter); x adalah jarak pergerakan pegas dari posisi normalnya (dalam unit meter).

Hukum Hooke utuk pegas yang bergerak secara vertikal

Robert Hooke menemukan bahwa pertambahan panjang pada pegas berbanding lurus dengan gaya yang di berikan dan bergantung pada karakteristik dari pegas tersebut.

Gambar 1. Pertambahan panjang ketika pegas diberi gaya

Dengan: F = Gaya yang diberikan pada pegas (N)

k = Tetapan gaya pegas (N/m)

= pertambahan panjang pegas (m)

Hukum Hooke juga berlaku untuk pada kawat atau benda elastis lainnya,

selama benda tersebut belum melampaui batas elastisitasnya.

Untuk lebih jelasnya berikut ini adalah link grafik animasi yang menjelaskan hubungan antara gaya versus elongasi.

http://webphysics.davidson.edu/applets/animator4/demo_hook.html

Pegas dapat ditarik dengan klik-drag bola biru seperti yang ditunjukkan pada animasi.

* Pada rentang berapakah kompresi dan peregangan berlaku hukum Hooke?

* Cari batas elastis pegas.

* Tentukan konstanta pegas dari pegas tersebut.

Karakteristik Pegas

Kinerja sebuah pegas ditandai dengan hubungan antara beban (F) diterapkan pada itu dan defleksi (δ) yang hasil, defleksi dari pegas kompresi yang diperhitungkan dari panjang bebas dibongkar seperti yang ditunjukkan pada animasi.

Karakteristik F-δ adalah sekitar linier disediakan pegas melingkar

dekat dan material elastis. Kemiringan karakteristik dikenal sebagai kekakuan (stiffness)dari pegas k = F / δ (aka. 'konstanta', atau 'tingkat', atau 'skala' atau 'gradient' pegas) dan ditentukan oleh geometri pegas dan modulus kekakuan seperti akan ditunjukkan. Batas hasil biasanya diatur untuk melebihi batas soliditas seperti digambarkan, sehingga tidak ada kemungkinan hasil dan perilaku non-linear akibatnya

bahkan jika pegas dipadatkan sementara perakitan sebelum operasi. Kadang-kadang pegas adalah sengaja dihasilkan atau pra-set selama manufaktur seperti yang akan dijelaskan nanti.

Animasi itu menggambarkan pegas bekerja antara keadaan operasional minimum (Flo, δlo) dan keadaan operasional maksimum (FHI, δhi) (penjelasan tata-nama). Jika jumlah siklus kecil - mengatakan kurang dari 104 - maka beban dapat diperlakukan sebagai statis, pertimbangan dinyatakan kelelahan berlaku.

Panjang kerja terbesar pegas harus appreciably kurang dari panjang bebas untuk menghindari semua kemungkinan kontak hilang antara pegas dan pelat, dengan shock konsekuen bila kontak adalah didirikan kembali. Dalam aplikasi frekuensi tinggi ini dapat dipenuhi oleh desain kendala FHI / Flo ≤ 3.

Sebagai pendekatan pegas solid, perbedaan pitch kecil antara kumparan akan menyebabkan kumparan kontak-untuk-coil progresif daripada kontak tiba-tiba antara semua gulungan secara bersamaan. Setiap kontak menyebabkan dampak dan kerusakan permukaan, dan peningkatan kekakuan. Untuk menghindari hal ini, panjang kerja pegas boleh melebihi panjang solid dengan clash allowance setidaknya 10% dari lendutan maksimum kerja - yang δs - δhi ≥ 0.1δhi, meskipun penyisihan ini mungkin perlu ditingkatkan di hadapan kecepatan tinggi dan / atau inertias.

JENIS RANGKAIAN PEGAS

Ada dua jenis rangkaian pegas yaitu rangkaian pegas seri dan rangkaian pegas paralel.

Rangkaian Pegas Seri

Pada rangkaian pegas yang dipasang seri dan diberikan gaya tarik akan terlihat bahwa pertambahan panjang total pegas ?x_total adalah jumlah dari pertambahan masing-masing panjang pegas.

Gambar 3. Rangakaian pegas seri

1/k_total= 1/k₁ + 1/k₂ + ... + 1/k_n

Dengan: k_total = tetapan gaya rangkaian total pegas yang tersusun seri (N/m)

k₁,k_2,k₃, … , k_n = tetapan gaya masing-masing komponen pegas (N/m)

Rangkaian Pegas Pararel

Sedangkan pada rangkaian pararel pegas bila diberikan gaya tarik akan terlihat bahwa pertambahan panjang masing-masing pegas sama dengan pertambahan total pegas. Dalam hal ini panjang pegas dan tetapan gaya pegas kita asumsikan sama.

Gambar 4. Rangkaian pegas Pararel

k_total = k1 + k₂ + k₃ + …+ k_n

Dengan: k_total = tetapan gaya rangkaian total pegas yang tersusun seri (N/m)

k₁,k_2,k₃, … , k_n = tetapan gaya masing-masing komponen pegas (N/m)

Sumber : mediafisika.com

Susunan-Pegas

Pegas (=spring) pegas - courtesy of Globalspec.inc

Untuk pegas yang tersusun seri sebagaimana gambar di samping
Untuk pegas yang tersusun paralel layaknya gambar aplikasi berikut :
pegas paralel depan mobil

Karena kedua pegas mendapatkan beban yang sama maka berlaku

y₁=y₂= 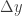$\Delta {y}$ sementara F₁+F₂ sebab kedua pegas tersebut membagi dua beban yang diterimanya.

Menjadikan W (beban) = F₁ + F₂

sehingga $\Delta y$ = $\frac{W}{k_{paralel}}$

${k} \Delta{y}$ = $k_{1}y_{1} + k_{2}y_{2}$

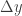
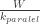
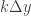
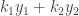
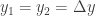
karena $y_{1} = y_{2} = \Delta {y}$ maka

${k} \Delta{y}$ = $k_{1} \Delta y + k_{2} \Delta {y}$

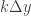
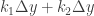
Secara distributif, ${k} \Delta{y} = ( k_{1} + k_{2} ) \Delta y$

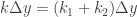
akhirnya ${k} = k_{1} + k_{2}$

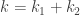
Analogi sederhana bisa perhatikan gambar di samping ini : physicsexperimental.org

Link : http://fisikarudy.com/pelajaran/susunan-pegas

Penerapan Elastisitas dalam kehidupan sehari-hari

Pada awal penjelasan mengenai hukum Hooke, kami telah berjanji akan membahas mengenai aplikasi elastisitas dalam kehidupan sehari-hari. Nah, berikut ini beberapa penerapan elastisitas dalam kehidupan kita.

Kita mulai dari teknologi yang sering kita gunakan, yaitu sepeda motor atau mobil.

Gambar disamping ini adalah pegas yang digunakan sebagai peredam kejutan pada kendaraan sepeda motor. Istilah kerennya pegas digunakan pada sistem suspensi kendaraan bermotor. Tujuan adanya pegas ini adalah untuk meredam kejutan ketika sepeda motor yang dikendarai melewati permukaan jalan yang tidak rata. Ketika sepeda motor melewati jalan berlubang, gaya berat yang bekerja pada pengendara (dan gaya berat motor) akan menekan pegas sehingga pegas mengalami mampatan. Akibat sifat elastisitas yang dimilikinya, pegas meregang kembali setelah termapatkan. Perubahan panjang pegas ini menyebabkan pengendara merasakan ayunan. Dalam kondisi ini, pengendara merasa sangat nyaman ketika sedang mengendarai sepeda motor. Pegas yang digunakan pada sepeda motor atau kendaraan lainnya telah dirancang untuk mampu menahan gaya berat sampai batas tertentu. Jika gaya berat yang menekan pegas melewati batas elastisitasnya, maka lama kelamaan sifat elastisitas pegas akan hilang. Oleh karena itu saran kami, agar pegas sepeda motor-mu awet muda, maka sebaiknya jangan ditumpangi lebih dari tiga orang.

Perancang sepeda motor telah memperhitungkan beban maksimum yang dapat diatasi oleh pegas (biasanya dua orang).

Pegas bukan hanya digunakan pada sistem suspensi sepeda motor tetapi juga pada kendaraan lainnya, seperti mobil, kereta api, dkk. (gambar kiri – per mobil)

Pada mobil, terdapat juga pegas pada setir kemudi (wah, belum punya gambarnya

). Untuk menghindari benturan antara pengemudi dengan gagang setir, maka pada kolom setir diberi pegas. Berdasarkan hukum I Newton (Hukum Inersia), ketika tabrakan terjadi, pengemudi (dan penumpang) cenderung untuk terus bergerak lurus. Nah, ketika pengemudi bergerak maju, kolom setir tertekan sehingga pegas memendek dan bergeser miring. Dengan demikian, benturan antara dada pengemudi dan setir dapat dihindari.

Karet Ketapel

Nah, contoh yang sangat sederhana dan mungkin sering anda temui adalah ketapel., ketapel adalah alat yang paling mujarab untuk membidik buah2an milik tetangga yang ranum dan mengundang selera. Sttt… jangan ditiru kalau dirimu tinggal di kota, kayanya tiap hari berurusan dengan game, ngenet, gamenet….gitu deh. ayo ngaku... paling ketapel juga ga tahu… hehe… piss.. lanjut. Ketika hendak menembak burung dengan ketapel misalnya, karet ketapel terlebih dahulu diregangkan (diberi gaya tarik). Akibat sifat elastisitasnya, panjang karet ketapelakan kembali seperti semula setelah gaya tarik dihilangkan.

Kasur Pegas

Contoh lain adalah kasur pegas. Ketika dirimu duduk atau tidur di atas kasur pegas, gaya beratmu menekan kasur. Karena mendapat tekanan maka pegas kasur termampatkan. Akibat sifat elastisitasnya, kasur pegas meregang kembali. Pegas akan meregang dan termampat, demikian seterusnya. Akibat adanya gaya gesekan maka suatu saat pegas berhenti bergerak. Dirimu yang berada di atas kasur merasa sangat empuk akibat regangan dan mampatan yang dialami oleh pegas kasur.

Dinamometer

Pernahkah dirimu melihat dinamometer ? mudah-mudahan di laboratorium fisika sekolah anda ada. Dinamometer, sebagaimana tampak pada gambar di samping adalah alat pengukur gaya. Biasanya digunakan untuk menghitung besar gaya pada percobaan di laboratorium. Di dalam dinamometer terdapat pegas. Pegas tersebut akan meregang ketika dikenai gaya luar. Misalnya anda melakukan percobaan mengukur besar gaya gesekan. Ujung pegas anda kaitkan dengan sebuah benda bermassa. Ketika benda ditarik, maka pegas meregang. Regangan pegas tersebut menunjukkan ukuran gaya, di mana besar gaya ditunjukkan oleh jarum pada skala yang terdapat pada samping pegas.

Timbangan

Pernahkah anda mengukur berat badan ? timbangan yang anda gunakan untuk mengukur berat badan (dalam fisika, berat yang dimaksudkan di sini adalah massa) juga memanfaatkan bantuan pegas. Pegas lagi, pegas lagi… hidup kita selalu ditemani oleh pegas. Neraca pegas yang digunakan untuk mengukur berat badan, terdapat juga neraca pegas yang lain (gambar kanan – neraca pegas buah)

Masih ada contoh lain yang berkaian dengan elastisitas pegas. Pernah fitness ? bagi pria-pria perkasa yang terlihat macho dengan otot lengan yang kuat dan dada bidang

, pasti pernah menggunakan alat tersebut. wah, ayo tebak… alat apakah itu ? alat tersebut terbuat dari pegas. Yang ini PR ya ?

Penerapan elastisitas benda padat pada konstruksi bangunan

Ada yang bercita-cita menjadi arsitek atau ahli bangunan ? pahami penjelasan ini secara baik ya, sebagai bekal di hari tua

Pada pembahasan mengenai tarikan, tekanan dan geseran, kita telah belajar mengenai perubahan bentuk pada setiap benda padat akibat adanya tegangan yang dialami benda tersebut. Ketika sebuah benda diberikan gaya luar maka akan timbul gaya dalam alias gaya internal pada benda itu sendiri. Ini adalah gaya tegangan yang telah dijelaskan sebelumnya.

Salah satu pemanfaatan sifat elastisitas benda padat dalam konstruksi bangunan adalah berkaitan dengan teknik memperluas ruangan. Berikut ini beberapa cara yang digunakan ahli bangunan dalam memperluas ruang sebuah bangunan (rumah, dkk). Mari kita bahas satu persatu….

Tiang dan Balok penyanggah pada pintu

Setiap rumah atau bangunan lainnya pasti memiliki pintu atau penghubung ruangan yang bentuknya seperti gambar di bawah. Kebanyakan bangunan menggunakan batu dan bata sebagai bahan dasar (disertai campuran semen dan pasir).

penerapan-elastisitas-dalam-kehidupan-01

Persoalannya, batu dan bata sangat lemah terhadap tarikan dan geseran walaupun kuat terhadap tekanan. Dirimu bisa membuktikan hal ini. Jika disekitar tempatmu terdapat batu dan bata, jika batu dan bata ditumpuk (disusun secara vertikal) dalam jumlah banyak, batu dan bata tidak mudah patah (bentuknya tetap seperti semula). Dalam hal ini batu dan bata sangat kuat terhadap tekanan. Tetapi jika batu dan bata mengalami tegangan tarik dan tegangan geser, batu dan bata mudah patah. Oleh karena itu digunakan balok untuk mengatasi masalah ini. Balok mampu mengatasi tegangan tarik, tegangan tekan dan tegangan geser. Jika anda amati balok penyanggah pada pintu rumah, tampak bahwa balok tersebut tidak berubah bentuk. Sebenarnya terdapat perubahan bentuk balok (amati gambar di bawah), hanya perubahannya sangat kecil sehingga tidak tampak ketika dilihat dari jauh. Bagian atas balok mengalami mampatan akibat adanya tegangan tekan yang disebabkan beban di atasnya (batu dan bata dkk), sedangkan bagian bawah balok mengalami pertambahan panjang (akibat tegangan tarik). Tegangan geser terjadi di dalam balok.

penerapan-elastisitas-dalam-kehidupan-02

Lengkungan setengah lingkaran

Pernahkah dirimu melihat pintu atau penhubung ruang sebuah bangunan seperti tampak pada gambar di bawah ? lengkungan setengah lingkaran ini pertama kali diperkenalkan oleh orang romawi. Apabila dirancang dengan baik maka batu-batu yang disusun melengkung mengalami tegangan tekan (batu-batu saling berdempetan) sehingga dapat menahan beban berat yang ada di atasnya. Ingat ya, batu sangat kuat terhadap tekanan.

penerapan-elastisitas-dalam-kehidupan-03

Sekian ya, kalo dirimu belum paham, coba baca kembali secara perlahan-lahan. Saran dari gurumuda, sebaiknya baca semua materi secara berurutan seperti yang telah diurutkan di bawah. Alasannya, setiap konsep yang dijelaskan sebelumnya sangat penting untuk pembahasan berikutnya. Kalo dirimu belum pelajari pembahasan sebelumnya, ntar malah gak nyambung…..

-------------------------------------------------------------------------------------------------------------------------------------

Penerapan Hukum Hooke dalam Kebijakan Investasi dari Bapak Pratolo:

The Principle of Hooke’s Law on Investing

Persamaan fisika favorit saya bukanlah E = m.c²Einstein. Persamaan fisika favorit saya adalah persamaan si jenius Hooke.

Hukum fisika fenomenal bagi saya bukanlah Hukum Relativitas. Hukum fisika fenomenal bagi saya adalah Hukum Elastisitas Hooke.

Hukum Hooke dinyatakan dalam persamaan Hooke:

F = - k.x

F = force, adalah gaya pegas yg timbul akibat deformasi (tarikan atau tekanan) (satuan: Newton)

x = jarak deformasi, yg ditimbulkan oleh gaya F, dari posisi kesetimbangan pegas (satuan: meter)

k = konstanta pegas yg menandakan elastisitas pegas (satuan: Newton/meter). Makin besar k, makin elastis pegas.

Tanda negatif menunjukkan arah gaya yg berlawanan dengan arah tarikan/tekanan x. Tanda ini menunjukkan gaya lenting (restoring force) pegas untuk kembali ke kesetimbangan.

Dalam investasi hukum Hooke amat sangat berguna bagi kita dalam memilih saham.

x = tekanan pasar saat siklus ekonomi memburuk / sentiment pasar negatif / bearish

atau lonjakan pasar saat siklus ekonomi mengembang / sentimen positif / bullish

k = value perusahaan.

Makin bernilai sebuah perusahaan maka k makin besar = makin elastis dalam menghadapi tekanan ekonomi = makin cepat pulih dari resesi.

Jika diintegralkan, maka persamaan Hooke menjadi Energi Potensial Pegas (Elastic Potential Energy)

U_e = ~ kx dx = ½ k.x²

Dalam investasi persamaan di atas berarti: potensial return saham suatu perusahaan sebanding dengan value perusahaan (k) dan sebanding dengan kuadrat sentimen pasar (x)

Berkat pendekatan Hukum Hooke ini, maka Anda tak perlu takut lagi berinvestasi pada masa krisis. Makin tertekan pasar akibat krisis ekonomi atau resesi, maka makin besar pula potensi return yg akan kita peroleh, asalkan kita memilih perusahaan dengan value tinggi.

Bagaimana memilih perusahaan yg mempunyai nilai k (value) tinggi?

Sederhana saja. Value sebuah perusahaan diukur dari 3 indikator fundamental:

Earning
Cash flow
Book value

Ikuti terus pratolo.com utk mengetahui bagaimana cara mengukur k ini.

(He..he.. hebat euy) sumber aslinya klik disini.

Link-link yang berkaitan
http://id.wikipedia.org/wiki/Hukum_Hooke
http://school.mech.uwa.edu.au/~dwright/DANotes/springs/intro/intro.html
http://www.scribd.com/doc/21960927/Gaya-Pegas
http://www.scribd.com/doc/17628480/Hukum-Hooke
http://www.scribd.com/doc/16673482/hukumhookeelastisitas

........................P r i m a S p r i n g s

MENU

Translator

DALAM BAHASA SUNDA

Senin, 17 Mei 2010

FLOODGATE

Selasa, 11 Mei 2010

ALBUMKU

Sabtu, 08 Mei 2010

Intermezzo

Kamis, 06 Mei 2010

Hukum Hooke